Propagation des erreurs
Dans les leçons précédentes, nous avons étudié les différentes sources d'erreurs en calcul numérique : erreurs de mesure, erreurs d'arrondi, erreurs de troncature. Une question fondamentale se pose maintenant : lorsqu'on effectue des calculs avec des données entachées d'erreurs, comment ces erreurs affectent-elles le résultat final ? Cette leçon développe les outils mathématiques permettant de répondre à cette question cruciale.
Position du problème
Le contexte pratique
Considérons une situation courante en ingénierie ou en sciences expérimentales. On dispose d'une grandeur mesurée , connue avec une certaine incertitude :
où représente la valeur mesurée (ou calculée) et l'erreur absolue associée.
On souhaite calculer une fonction de cette grandeur. La question est : quelle est l'incertitude sur ?
Autrement dit, on cherche à déterminer tel que :
Un exemple introductif
Supposons que l'on mesure le côté d'un carré : cm. Quelle est l'incertitude sur l'aire ?
L'aire calculée est cm². Mais l'aire réelle pourrait être comprise entre :
L'incertitude sur l'aire est donc d'environ cm², soit 2 % — alors que l'incertitude sur le côté n'était que de 1 %. L'erreur s'est amplifiée en passant par la fonction carré.
Ce phénomène d'amplification (ou parfois d'atténuation) des erreurs est précisément ce que nous allons quantifier.
Propagation au premier ordre : une variable
Dérivation de la formule fondamentale
Soit une fonction dérivable et une grandeur connue avec incertitude. Nous cherchons l'incertitude sur .
L'idée clé consiste à utiliser un développement de Taylor au premier ordre. Au voisinage de , on peut écrire :
Puisque peut s'écarter de d'au plus , l'écart maximal sur est :
On obtient ainsi la formule de propagation des erreurs au premier ordre :
Formule de propagation (une variable)
Si et est une fonction dérivable, alors :
avec :
La valeur absolue garantit que l'incertitude est toujours positive.
Interprétation géométrique
Cette formule admet une interprétation géométrique élégante. La dérivée représente la pente de la tangente à la courbe au point .
- Si la pente est forte (en valeur absolue), une petite variation de entraîne une grande variation de : l'erreur est amplifiée.
- Si la pente est faible, l'erreur est atténuée. Par exemple, la fonction a une dérivée qui diminue quand augmente : pour de grandes valeurs, l'erreur sur se traduit par une erreur plus petite sur .
- Si la pente est nulle (extremum), l'erreur est minimale au premier ordre.
Propagation des erreurs : F(x) = x²
Interprétation : La pente est forte (|F'| = 4.0 > 2). Une erreur de ±0.30 sur X produit une erreur de ±1.20 sur F. L'erreur est amplifiée d'un facteur 4.0.
Exemple détaillé : la racine carrée
Considérons la fonction avec possédant 4 chiffres significatifs exacts.
Étape 1 : Déterminer l'erreur sur X
Avec 4 CSE, l'erreur absolue est bornée par la moitié de l'unité du dernier chiffre :
Donc .
Étape 2 : Calculer F(X*)
Étape 3 : Calculer la dérivée de F
Étape 4 : Évaluer la dérivée en X*
Étape 5 : Calculer l'erreur propagée
Conclusion :
Le résultat possède également 4 chiffres significatifs exacts. Dans ce cas, la précision relative a été approximativement conservée.
Formule en termes d'erreurs relatives
Il est souvent utile d'exprimer la propagation en termes d'erreurs relatives. Définissons :
En partant de , on obtient :
Le coefficient est appelé coefficient d'amplification de l'erreur relative.
Exemples de coefficients d'amplification
| Fonction F(X) | Coefficient d'amplification | Commentaire |
|---|---|---|
| L'erreur relative est multipliée par n | ||
| L'erreur relative est divisée par 2 | ||
| Amplification proportionnelle à X | ||
| Atténuation si | ||
| Variable selon X |
La méthode de la fourchette
Principe
La méthode de la fourchette (ou méthode des bornes) offre une alternative à l'approche par les dérivées. Elle est particulièrement utile lorsque la fonction est monotone mais difficile à dériver, ou lorsqu'on souhaite une borne rigoureuse plutôt qu'une approximation.
Principe : Si et si est continue et monotone sur , alors :
Pour une fonction croissante : .
Pour une fonction décroissante : .
Exemple : reprise de la racine carrée
Reprenons l'exemple précédent avec .
L'intervalle de confiance pour est .
La fonction racine carrée étant croissante sur , on calcule :
Donc .
Le milieu de cet intervalle est et la demi-largeur est .
On obtient : .
Remarque : Les deux méthodes donnent ici des résultats très proches (). La légère différence provient du fait que la méthode des dérivées est une approximation au premier ordre, tandis que la méthode de la fourchette donne un encadrement exact.
Comparaison des deux méthodes
| Critère | Méthode des dérivées | Méthode de la fourchette |
|---|---|---|
| Précision | Approximation (premier ordre) | Exacte (si monotone) |
| Calculs requis | Une dérivée, une évaluation | Deux évaluations de F |
| Conditions | F dérivable | F continue et monotone |
| Généralisation | Facile à plusieurs variables | Complexe à plusieurs variables |
Conseil pratique
La méthode des dérivées est généralement préférée pour sa simplicité et sa facilité de généralisation. La méthode de la fourchette est utile pour vérifier un résultat ou lorsqu'on a besoin d'une borne rigoureuse.
Propagation à plusieurs variables
Généralisation de la formule
Dans de nombreuses situations pratiques, une grandeur dépend de plusieurs variables mesurées. Considérons une fonction de deux variables, où :
En utilisant un développement de Taylor à deux variables au premier ordre :
L'erreur maximale sur est obtenue lorsque les deux termes d'erreur s'additionnent (cas le plus défavorable) :
Formule de propagation (plusieurs variables)
Pour une fonction de variables indépendantes :
où les dérivées partielles sont évaluées au point .
Exemple pratique : mesure d'une hauteur par triangulation
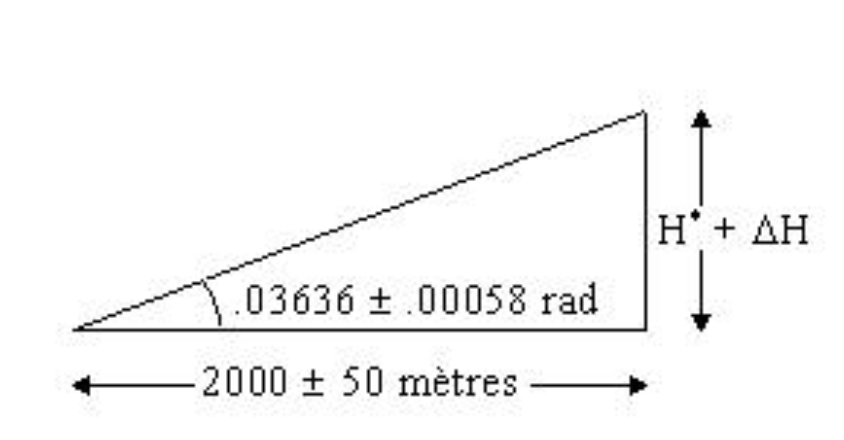
Un géomètre souhaite déterminer la hauteur d'un bâtiment. Il mesure la distance horizontale au pied du bâtiment et l'angle d'élévation vers le sommet.
La hauteur est donnée par :
Les mesures sont :
- m avec m
- rad (environ 2,08°) avec rad
Étape 1 : Calculer H*
Étape 2 : Calculer les dérivées partielles
Étape 3 : Évaluer les dérivées partielles
Étape 4 : Calculer l'erreur propagée
Conclusion :
Le résultat ne possède que 2 chiffres significatifs, bien que les mesures initiales semblaient plus précises. Cet exemple illustre comment les erreurs se combinent et peuvent dégrader significativement la précision finale.
Analyse des contributions :
- Contribution de l'erreur sur : 1,82 m (61 %)
- Contribution de l'erreur sur : 1,16 m (39 %)
L'erreur sur la distance contribue davantage à l'incertitude finale. Pour améliorer la précision, il faudrait prioritairement réduire l'erreur sur .
Règles pour les opérations arithmétiques
Les formules générales se simplifient considérablement pour les quatre opérations arithmétiques de base. Ces règles simplifiées sont d'usage constant en pratique.
Addition :
Appliquons la formule générale avec :
Donc :
Règle de l'addition
L'erreur absolue sur une somme est la somme des erreurs absolues.
Soustraction :
Avec :
Donc :
Règle de la soustraction
L'erreur absolue sur une différence est également la somme des erreurs absolues.
Attention : les erreurs s'additionnent, elles ne se compensent pas !
Lien avec l'annulation catastrophique
Cette règle explique mathématiquement le phénomène d'annulation catastrophique. Lors d'une soustraction où , le résultat est petit, mais l'erreur absolue reste inchangée. L'erreur relative explose donc.
Multiplication :
Avec :
Donc :
En divisant par , on obtient l'erreur relative :
Règle de la multiplication
L'erreur relative sur un produit est la somme des erreurs relatives.
Division :
Avec :
Donc :
En divisant par :
Règle de la division
L'erreur relative sur un quotient est la somme des erreurs relatives.
Tableau récapitulatif
| Opération | Erreur absolue | Erreur relative |
|---|---|---|
| Non additive | ||
| Non additive (attention !) | ||
Règles mnémotechniques :
- Pour l'addition et la soustraction : on additionne les erreurs absolues.
- Pour la multiplication et la division : on additionne les erreurs relatives.
L'importance de la formulation
Un exemple révélateur
Considérons le calcul de avec :
Méthode 1 : Calcul direct
Résultat :
Méthode 2 : Factorisation préalable
On utilise l'identité remarquable :
Posons et . Alors .
Calculons les erreurs sur et :
Pour le produit :
Résultat :
Comparaison des résultats
| Méthode | Erreur estimée |
|---|---|
| Calcul direct | ± 1,12 |
| Après factorisation | ± 1,6 |
Les deux méthodes donnent des estimations d'erreur différentes ! Cela peut sembler paradoxal, mais s'explique par le fait que la formule de propagation au premier ordre fournit une borne supérieure de l'erreur, qui dépend de la façon dont on décompose le calcul.
À retenir
La formule de propagation des erreurs donne une majoration de l'erreur, pas sa valeur exacte. Cette majoration suppose que toutes les erreurs s'additionnent dans le sens le plus défavorable, ce qui est rarement le cas en pratique. Des analyses plus fines (propagation quadratique, méthodes statistiques) permettent d'obtenir des estimations plus réalistes.
Implémentation en Python
import math
def propager_erreur_1var(f, df, x_val, delta_x):
"""
Propage l'erreur pour une fonction à une variable.
Paramètres :
f : fonction à évaluer
df : dérivée de la fonction
x_val : valeur de x
delta_x : erreur absolue sur x
Retourne :
(f_val, delta_f) : valeur et erreur propagée
"""
f_val = f(x_val)
delta_f = abs(df(x_val)) * delta_x
return f_val, delta_f
def propager_erreur_2var(f, df_dx, df_dy, x_val, y_val, delta_x, delta_y):
"""
Propage l'erreur pour une fonction à deux variables.
"""
f_val = f(x_val, y_val)
delta_f = abs(df_dx(x_val, y_val)) * delta_x + abs(df_dy(x_val, y_val)) * delta_y
return f_val, delta_f
# Exemple 1 : Racine carrée
print("=== Exemple 1 : Racine carrée ===")
f = lambda x: math.sqrt(x)
df = lambda x: 1 / (2 * math.sqrt(x))
x_val, delta_x = 1.234, 0.0005
f_val, delta_f = propager_erreur_1var(f, df, x_val, delta_x)
print(f"X = {x_val} ± {delta_x}")
print(f"F(X) = √X = {f_val:.6f} ± {delta_f:.6f}")
print()
# Exemple 2 : Hauteur par triangulation
print("=== Exemple 2 : Triangulation ===")
H = lambda L, theta: L * math.tan(theta)
dH_dL = lambda L, theta: math.tan(theta)
dH_dtheta = lambda L, theta: L / (math.cos(theta) ** 2)
L_val, delta_L = 2000, 50
theta_val, delta_theta = 0.03636, 0.00058
H_val, delta_H = propager_erreur_2var(
H, dH_dL, dH_dtheta,
L_val, theta_val,
delta_L, delta_theta
)
print(f"L = {L_val} ± {delta_L} m")
print(f"θ = {theta_val} ± {delta_theta} rad")
print(f"H = L·tan(θ) = {H_val:.1f} ± {delta_H:.1f} m")
print()
# Exemple 3 : Les quatre opérations
print("=== Exemple 3 : Opérations arithmétiques ===")
U, delta_U = 10.0, 0.05
V, delta_V = 2.0, 0.03
# Addition
somme = U + V
delta_somme = delta_U + delta_V
print(f"U + V = {somme} ± {delta_somme}")
# Soustraction
diff = U - V
delta_diff = delta_U + delta_V
print(f"U - V = {diff} ± {delta_diff}")
# Multiplication
prod = U * V
delta_prod = abs(V) * delta_U + abs(U) * delta_V
print(f"U × V = {prod} ± {delta_prod}")
# Division
quot = U / V
delta_quot = delta_U / abs(V) + abs(U) * delta_V / (V ** 2)
print(f"U / V = {quot} ± {delta_quot:.4f}")Synthèse
La propagation des erreurs est un outil essentiel pour évaluer la fiabilité d'un résultat numérique. Les points clés à retenir sont :
-
Formule fondamentale : L'erreur se propage selon pour une variable, et se généralise par sommation des contributions pour plusieurs variables.
-
Règles simplifiées : Pour l'addition et la soustraction, on additionne les erreurs absolues. Pour la multiplication et la division, on additionne les erreurs relatives.
-
La soustraction est dangereuse : C'est la seule opération qui peut amplifier dramatiquement l'erreur relative (annulation catastrophique).
-
La formulation compte : Deux expressions mathématiquement équivalentes peuvent conduire à des estimations d'erreur différentes.
-
C'est une majoration : La formule de propagation donne une borne supérieure de l'erreur, souvent pessimiste.
Exercices
Exercice 1 : Propagation simple
On mesure le rayon d'un cercle : cm.
- Calculez l'aire et son incertitude.
- Calculez le périmètre et son incertitude.
- Comparez les erreurs relatives sur et . Laquelle est la plus grande ? Expliquez pourquoi.
Exercice 2 : Plusieurs variables
La résistance équivalente de deux résistances en parallèle est :
On mesure Ω et Ω.
- Calculez et son incertitude en utilisant la formule de propagation générale.
- Vérifiez votre résultat en décomposant le calcul : posez et , puis calculez .
Exercice 3 : Comparaison des méthodes
Pour , calculez :
- Par la formule de propagation au premier ordre.
- Par la méthode de la fourchette.
- Comparez les deux résultats et commentez.
Exercice 4 : Annulation catastrophique revisitée
Soient et .
- Calculez et son incertitude.
- Calculez l'erreur relative sur le résultat.
- Comparez avec les erreurs relatives initiales sur et .
- Expliquez le phénomène observé.
Exercice 5 : Application pratique
La vitesse du son dans l'air est donnée approximativement par :
où est la température en degrés Celsius et est en m/s.
On mesure °C.
- Calculez la vitesse du son et son incertitude.
- Quelle précision sur faudrait-il pour obtenir avec une erreur inférieure à 0,1 m/s ?