Introduction aux systèmes linéaires et notation matricielle

Objectifs d'apprentissage

À la fin de cette leçon, vous serez en mesure de :

Reconnaître un système d'équations linéaires dans différents contextes applicatifs
Exprimer un système linéaire sous forme matricielle
Manipuler les matrices selon les règles fondamentales de l'algèbre linéaire
Expliquer pourquoi la méthode de Cramer est impraticable pour les grands systèmes

Prérequis

Notions de base en algèbre linéaire (matrices, vecteurs)
Opérations élémentaires sur les matrices (addition, multiplication)

Pourquoi résoudre des systèmes linéaires ?

Les systèmes d'équations linéaires apparaissent dans une multitude de domaines scientifiques et techniques. Comprendre comment les résoudre efficacement est fondamental pour tout ingénieur ou scientifique.

Exemple concret : un circuit électrique

Considérons le circuit électrique suivant. Une source de tension $V$ alimente un réseau de résistances, et nous souhaitons déterminer les intensités de courant $i_1, i_2, i_3, i_4, i_5$ dans chaque branche.

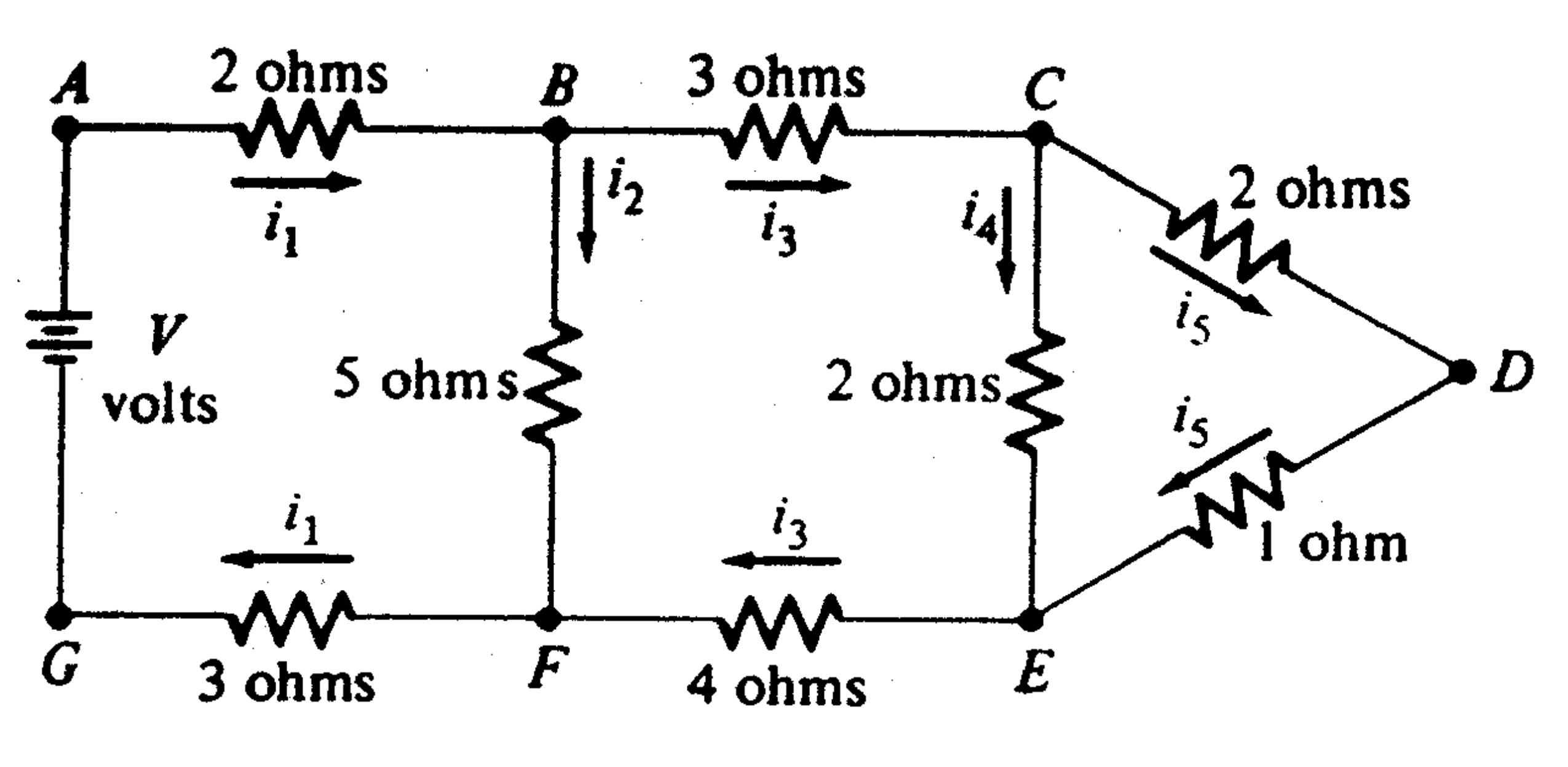
Circuit électrique avec 5 courants

Pour analyser ce circuit, nous utilisons les lois fondamentales de l'électricité.

Rappel des lois de l'électricité

La loi d'Ohm établit que la tension $U$ aux bornes d'une résistance est proportionnelle au courant $I$ qui la traverse :

U = R \cdot I

Par exemple, si un courant $i_1$ traverse une résistance de 2 ohms, la chute de tension est $2 i_1$ volts.

Les lois de Kirchhoff traduisent deux principes physiques fondamentaux :

Loi des nœuds (conservation de la charge) : à tout nœud du circuit, la somme des courants entrants égale la somme des courants sortants. Le courant électrique ne peut ni s'accumuler ni disparaître en un point.
Loi des mailles (conservation de l'énergie) : le long de tout chemin fermé (maille), la somme algébrique des tensions est nulle. En parcourant une maille complète, on revient au même potentiel électrique.

Application au circuit

Appliquons ces lois à notre circuit.

Conservation du courant aux nœuds :

Au nœud B, le courant $i_1$ arrivant de la source se divise en deux : une partie $i_2$ descend vers F, et une partie $i_3$ continue vers C. Cela donne :

i_1 = i_2 + i_3 \quad \Leftrightarrow \quad i_1 - i_2 - i_3 = 0

De même, au nœud C, le courant $i_3$ se divise entre $i_4$ (vers E) et $i_5$ (vers D) :

i_3 = i_4 + i_5 \quad \Leftrightarrow \quad i_3 - i_4 - i_5 = 0

Bilan des tensions dans les mailles :

Parcourons la maille gauche A-B-F-G-A dans le sens horaire. On part de la source ( $+V$ ), on traverse la résistance de 2Ω entre A et B ( $-2i_1$ ), puis celle de 5Ω entre B et F ( $-5i_2$ ), et enfin celle de 3Ω entre G et F ( $-3i_1$ ) :

V - 2i_1 - 5i_2 - 3i_1 = 0 \quad \Rightarrow \quad 5i_1 + 5i_2 = V

Pour la maille centrale B-C-E-F-B, en partant de B vers C (résistance 3Ω parcourue par $i_3$ ), puis C vers E (2Ω avec $i_4$ ), E vers F (4Ω avec $i_3$ ), et retour F vers B (5Ω avec $i_2$ dans le sens opposé) :

- 3i_3 - 2i_4 - 4i_3 + 5i_2 = 0 \quad \Rightarrow \quad 5i_2 - 7i_3 - 2i_4 = 0

Enfin, la maille droite C-D-E-C contient les résistances de 2Ω et 1Ω (parcourues par $i_5$ ) et celle de 2Ω (parcourue par $i_4$ en sens opposé) :

- 2i_5 - i_5 + 2i_4 = 0 \quad \Rightarrow \quad 2i_4 - 3i_5 = 0

Le système linéaire

Nous obtenons ainsi 5 équations pour 5 inconnues :

\begin{cases} 5i_1 + 5i_2 = V \\ i_1 - i_2 - i_3 = 0 \\ i_3 - i_4 - i_5 = 0 \\ 5i_2 - 7i_3 - 2i_4 = 0 \\ 2i_4 - 3i_5 = 0 \end{cases}

Ce système peut s'écrire sous forme matricielle $A \cdot x = b$ :

\begin{pmatrix} 5 & 5 & 0 & 0 & 0 \\ 1 & -1 & -1 & 0 & 0 \\ 0 & 0 & 1 & -1 & -1 \\ 0 & 5 & -7 & -2 & 0 \\ 0 & 0 & 0 & 2 & -3 \end{pmatrix} \begin{pmatrix} i_1 \\ i_2 \\ i_3 \\ i_4 \\ i_5 \end{pmatrix} = \begin{pmatrix} V \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix}

L'enjeu : ce système de 5 équations peut sembler simple à résoudre à la main. Mais en pratique, les circuits électroniques réels contiennent des milliers, voire des millions de composants. Par exemple, un microprocesseur moderne intègre des dizaines de milliards de transistors ! Développer des méthodes numériques efficaces pour résoudre ces grands systèmes est donc essentiel — c'est précisément l'objet de ce chapitre.

Autres domaines d'application

Les systèmes linéaires interviennent notamment dans :

Domaine	Application typique
Génie civil	Calcul des tensions dans une structure
Hydraulique	Analyse du flot dans un réseau de canalisations
Chimie	Équilibrage de réactions, mélange de produits
Mécanique	Vibration d'un système, analyse modale
Thermique	Transfert de chaleur, distribution de température
Mathématiques appliquées	Résolution numérique d'équations différentielles

Notation matricielle

Du système d'équations à la forme matricielle

Considérons un système de deux équations à deux inconnues :

a_{11}x_1 + a_{12}x_2 = b_1

a_{21}x_1 + a_{22}x_2 = b_2

Ce système peut s'écrire de manière compacte sous forme matricielle :

\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}

Ou encore plus simplement :

A \cdot x = b

où :

$A$ est la matrice des coefficients (dimensions $n \times n$ )
$x$ est le vecteur des inconnues (dimensions $n \times 1$ )
$b$ est le vecteur des seconds membres (dimensions $n \times 1$ )

La notation matricielle permet de manipuler des systèmes de grande taille (des centaines, voire des millions d'équations) de manière uniforme et compacte. Les algorithmes que nous étudierons s'appliquent quelle que soit la dimension du système.

Quand un système admet-il une solution ?

Avant de chercher à résoudre un système, il est essentiel de comprendre dans quelles conditions une solution existe.

Nombre d'équations et d'inconnues

Considérons un système de $m$ équations à $n$ inconnues. Trois cas se présentent :

Cas 1 : Système carré ( $m = n$ )

Lorsque le nombre d'équations égale le nombre d'inconnues, le système peut admettre une solution unique. C'est le cas le plus favorable, celui sur lequel nous nous concentrerons dans ce chapitre. Par exemple, notre circuit électrique avec 5 équations et 5 courants inconnus entre dans cette catégorie.

Cas 2 : Système surdéterminé ( $m > n$ )

Plus d'équations que d'inconnues. En général, aucune solution exacte n'existe car les contraintes sont trop nombreuses. On cherche alors une solution approchée qui minimise l'erreur — c'est le domaine des moindres carrés, que nous aborderons dans la leçon sur les systèmes rectangulaires.

Cas 3 : Système sous-déterminé ( $m < n$ )

Moins d'équations que d'inconnues. Il y a trop de degrés de liberté : si une solution existe, elle n'est pas unique. On obtient une infinité de solutions formant un espace de dimension $n - m$ .

Condition nécessaire mais pas suffisante

Avoir autant d'équations que d'inconnues ( $m = n$ ) est nécessaire pour espérer une solution unique, mais ce n'est pas suffisant. Considérons le système :

\begin{cases} x + y = 1 \\ 2x + 2y = 3 \end{cases}

La seconde équation devrait être le double de la première, mais $3 \neq 2 \times 1$ . Les deux droites sont parallèles et ne se croisent jamais : le système n'a aucune solution.

À l'inverse, si la seconde équation était $2x + 2y = 2$ , les deux équations seraient équivalentes (la seconde est le double de la première). On aurait alors une infinité de solutions : tous les points de la droite $x + y = 1$ .

La notion de rang

Pour qu'un système carré $A \cdot x = b$ admette une solution unique, il faut que les $n$ équations soient linéairement indépendantes — c'est-à-dire qu'aucune ne puisse s'exprimer comme combinaison des autres. Cette condition se traduit par :

\text{rang}(A) = n \quad \Leftrightarrow \quad \det(A) \neq 0

Nous approfondirons ces notions de rang et de déterminant dans la leçon sur la singularité des matrices. Pour l'instant, retenons que les méthodes numériques que nous allons étudier détecteront automatiquement les cas problématiques (systèmes singuliers).

Rappels essentiels sur les matrices

Pour manipuler correctement les systèmes linéaires, il est essentiel de maîtriser les propriétés fondamentales des matrices.

Multiplication de matrices

Deux matrices $A$ et $B$ peuvent être multipliées si elles sont conformes : si $A$ est de dimension $K \times L$ et $B$ est de dimension $M \times N$ , alors le produit $A \cdot B$ existe si et seulement si $L = M$ . Le résultat est une matrice de dimension $K \times N$ .

Propriétés algébriques

Propriété	Formule	Remarque
Associativité	$A \cdot (B \cdot C) = (A \cdot B) \cdot C$	Toujours vraie
Non-commutativité	$A \cdot B \neq B \cdot A$	En général
Distributivité	$A \cdot (B + C) = A \cdot B + A \cdot C$	Toujours vraie

⚠️

Attention à l'ordre de multiplication

Contrairement aux nombres réels, le produit matriciel n'est pas commutatif. L'ordre dans lequel on multiplie les matrices est crucial. Par exemple, $A \cdot B$ et $B \cdot A$ donnent généralement des résultats différents (et peuvent même ne pas être tous deux définis).

Matrices particulières

Matrice identité $I$ : matrice carrée avec des 1 sur la diagonale et des 0 ailleurs. Elle joue le rôle du nombre 1 pour la multiplication :

A \cdot I = I \cdot A = A

Matrice nulle $0$ : matrice dont tous les éléments sont nuls. Elle joue le rôle du nombre 0 :

A + 0 = A \quad \text{et} \quad A \cdot 0 = 0

Transposée $A^T$ : matrice obtenue en interchangeant les lignes et les colonnes de $A$ . Si $A$ est de dimension $m \times n$ , alors $A^T$ est de dimension $n \times m$ .

Trace : somme des éléments diagonaux d'une matrice carrée :

\text{tr}(A) = \sum_{i=1}^{n} a_{ii}

La méthode de Cramer : élégante mais impraticable

Énoncé de la règle de Cramer

Pour un système $A \cdot x = b$ de $n$ équations à $n$ inconnues, si le déterminant de $A$ est non nul ( $\det(A) \neq 0$ ), alors le système admet une solution unique donnée par :

x_j = \frac{\det(A_j)}{\det(A)} \quad \text{pour } j = 1, 2, \ldots, n

où $A_j$ est la matrice obtenue en remplaçant la $j$ -ème colonne de $A$ par le vecteur $b$ .

Exemple pour un système 2×2

Soit le système :

\begin{cases} 3x_1 + 2x_2 = 7 \\ x_1 - x_2 = 1 \end{cases}

Calculons les déterminants :

\det(A) = \begin{vmatrix} 3 & 2 \\ 1 & -1 \end{vmatrix} = 3 \times (-1) - 2 \times 1 = -5

\det(A_1) = \begin{vmatrix} 7 & 2 \\ 1 & -1 \end{vmatrix} = -7 - 2 = -9

\det(A_2) = \begin{vmatrix} 3 & 7 \\ 1 & 1 \end{vmatrix} = 3 - 7 = -4

D'où : $x_1 = \frac{-9}{-5} = 1.8$ et $x_2 = \frac{-4}{-5} = 0.8$ .

Visualisez ce système de manière interactive :

Pourquoi la méthode de Cramer est-elle impraticable ?

🚨

Complexité prohibitive

La méthode de Cramer nécessite le calcul de $n+1$ déterminants de matrices $n \times n$ . Le calcul d'un déterminant par la méthode des cofacteurs a une complexité de $O(n!)$ . Pour un système de seulement 20 équations, le nombre d'opérations dépasse $20! \approx 2.4 \times 10^{18}$ , ce qui prendrait plusieurs décennies sur un ordinateur de bureau moderne, rendant cette approche totalement impraticable.

Le tableau suivant illustre l'explosion du coût de calcul :

Taille n	Nombre d'opérations (n!)	Temps estimé
5	120	Instantané
10	3 628 800	Quelques millisecondes
15	1.3 × 10¹²	Plusieurs heures
25	1.55 × 10²⁵	Des millions d'années

C'est pourquoi nous devons développer des méthodes numériques plus efficaces, comme l'élimination de Gauss ( $O(n^3)$ ), que nous étudierons dans les prochaines leçons.

Le graphique suivant illustre cette explosion combinatoire de manière frappante :

Résumé

Dans cette leçon, nous avons établi les fondements pour l'étude des systèmes linéaires :

Les systèmes d'équations linéaires apparaissent dans de nombreux domaines : circuits électriques, structures, transfert de chaleur, etc.
La notation matricielle $A \cdot x = b$ permet de représenter tout système linéaire de manière compacte.
Les matrices suivent des règles spécifiques : le produit est associatif mais non commutatif.
La méthode de Cramer, bien qu'élégante théoriquement, est impraticable en pratique à cause de sa complexité en $O(n!)$ .
Nous avons besoin de méthodes numériques efficaces pour résoudre les systèmes de grande taille.

Pour aller plus loin

Dans la prochaine leçon, nous étudierons les systèmes triangulaires, qui sont particulièrement simples à résoudre, ainsi que les opérations élémentaires qui permettent de transformer tout système en un système équivalent plus facile à résoudre.