Introduction à l'interpolation et méthode de collocation
Objectifs d'apprentissage
À la fin de cette leçon, vous serez en mesure de :
- Expliquer la différence entre interpolation et extrapolation
- Comprendre le principe de la méthode de collocation
- Énoncer et démontrer le théorème d'unicité du polynôme de collocation
- Identifier les applications pratiques de l'interpolation
Prérequis
- Notions de base sur les polynômes
- Propriétés des fonctions continues
Motivation : pourquoi interpoler ?
Dans de nombreuses applications scientifiques et techniques, nous disposons de mesures expérimentales ou de données tabulées en certains points, mais nous avons besoin d'estimer la valeur de la fonction en d'autres points.
Exemple concret : trajectoire d'une fusée
Considérons le problème suivant : une fusée est suivie par radar, et sa position est mesurée à intervalles réguliers. Entre deux mesures, nous devons estimer sa position pour assurer un suivi continu.
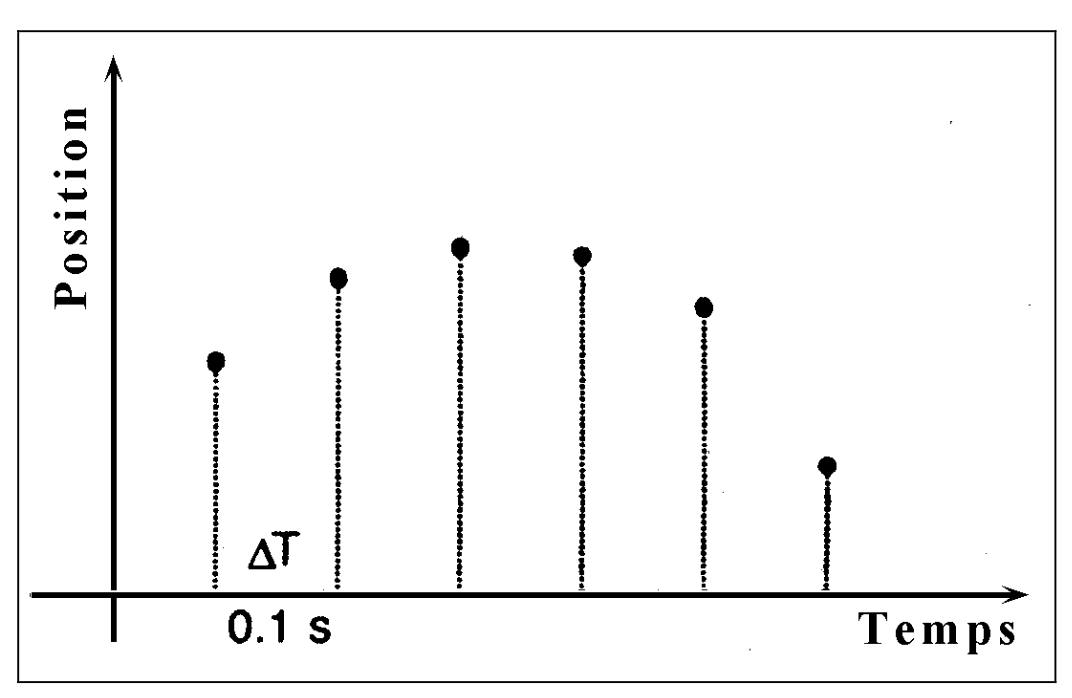
| Temps (ms) | Altitude (km) |
|---|---|
| 0 | 0 |
| 100 | 5.2 |
| 200 | 18.1 |
| 300 | 38.5 |
| 400 | 65.3 |
Question : Quelle est l'altitude à ?
Ce problème est un exemple typique d'interpolation : trouver une valeur entre des points connus.
Le problème d'interpolation
Estimer une fonction inconnue à partir de points connus
Interpolation vs extrapolation
Définitions
Interpolation
L'interpolation consiste à estimer la valeur d'une fonction en un point situé à l'intérieur de l'intervalle défini par les données connues.
Extrapolation
L'extrapolation consiste à estimer la valeur d'une fonction en un point situé à l'extérieur de l'intervalle des données connues. Cette opération est généralement moins fiable et plus risquée.
Illustration
Si nous avons des données pour :
- Calculer avec est une interpolation
- Calculer avec ou est une extrapolation
Attention à l'extrapolation
L'extrapolation peut conduire à des erreurs importantes car le comportement de la fonction en dehors de l'intervalle des données est inconnu. Une tendance observée sur l'intervalle peut ne pas se poursuivre au-delà.
Danger de l'extrapolation
Le polynôme peut diverger rapidement hors de l'intervalle des données
Le principe de collocation
Idée fondamentale
La méthode de collocation consiste à construire un polynôme qui passe exactement par tous les points de données. Ce polynôme est appelé polynôme d'interpolation ou polynôme de collocation.
Observation clé
- 2 points déterminent une droite unique (polynôme de degré 1)
- 3 points (non alignés) déterminent une parabole unique (polynôme de degré 2)
- n+1 points déterminent un polynôme de degré n unique
Formulation mathématique
Soit points de données avec des abscisses distinctes.
On cherche un polynôme de degré au plus tel que :
Ces conditions sont appelées conditions de collocation.
Polynôme de collocation
Le polynôme de degré n passe exactement par n+1 points
| Point | x0 | x1 | x2 |
|---|---|---|---|
| xᵢ | 0 | 1 | 2 |
| f(xᵢ) | 1 | 2 | 0.5 |
Exemple : interpolation linéaire
Considérons deux points et .
Le polynôme de collocation de degré 1 est la droite passant par ces deux points :
Exemple numérique
Soit les points et .
Donc :
Vérification :
Exemple : interpolation quadratique
Avec trois points , on cherche un polynôme de degré 2 :
Les conditions de collocation donnent un système de 3 équations à 3 inconnues :
Exemple numérique
Soit les points .
Le système devient :
De la première équation :
De la deuxième :
De la troisième :
En résolvant : et
Donc :
Théorème d'existence et d'unicité
Théorème fondamental
Soit points avec des abscisses distinctes. Il existe un unique polynôme de degré au plus tel que pour tout .
Ce théorème comporte deux parties : l'existence (il existe un tel polynôme) et l'unicité (il n'y en a qu'un seul). Démontrons chacune séparément.
Démonstration de l'existence
Pour montrer qu'un polynôme de collocation existe, nous allons montrer que le système linéaire correspondant admet une solution. L'idée est de vérifier que la matrice de Vandermonde associée est inversible.
Formulation matricielle : Un polynôme de degré au plus s'écrit :
Les conditions de collocation donnent le système :
Cette matrice est appelée matrice de Vandermonde. Le système admet une solution unique si et seulement si .
Cas parabolique () : Illustrons le calcul avec 3 points. La matrice est :
Calculons son déterminant en soustrayant la première ligne aux autres :
En développant selon la première colonne, puis en factorisant :
Utilisons l'identité :
Cas général : On peut montrer que le déterminant de Vandermonde pour points est :
C'est le produit de toutes les différences pour .
Conclusion sur l'existence
Si toutes les abscisses sont distinctes, alors chaque facteur est non nul, donc . La matrice est inversible, et le système admet une unique solution. Le polynôme de collocation existe.
Démonstration de l'unicité
Nous allons démontrer l'unicité par raisonnement par l'absurde. Cette technique consiste à supposer que la conclusion est fausse, puis à montrer que cette supposition mène à une contradiction.
Hypothèse (par l'absurde) : Supposons qu'il existe deux polynômes distincts, et , tous deux de degré au plus , qui satisfont les mêmes conditions de collocation :
Étape 1 : Construction du polynôme différence
Définissons un nouveau polynôme comme la différence des deux :
Puisque et sont tous deux de degré au plus , leur différence est également un polynôme de degré au plus . (En effet, lorsqu'on soustrait deux polynômes, le degré du résultat ne peut pas excéder le degré maximal des deux polynômes.)
Étape 2 : Identification des racines de D(x)
Évaluons en chacun des points de collocation :
Cela signifie que chaque est une racine (ou zéro) du polynôme . Puisque les abscisses sont distinctes par hypothèse, le polynôme possède donc au moins racines distinctes.
Étape 3 : Application du théorème fondamental de l'algèbre
Rappelons un résultat fondamental de l'algèbre des polynômes :
Théorème (nombre maximal de racines)
Un polynôme non nul de degré possède au plus racines (comptées avec multiplicité).
Ce théorème découle du fait qu'un polynôme de degré peut s'écrire sous forme factorisée avec au plus facteurs linéaires.
Appliquons ce résultat à notre polynôme :
- est de degré au plus
- Or, possède racines distinctes
Si était un polynôme non nul de degré , il pourrait avoir au plus racines. Mais nous venons de montrer qu'il en possède . C'est une contradiction !
Étape 4 : Conclusion
La seule façon de résoudre cette contradiction est que soit le polynôme nul, c'est-à-dire :
En effet, le polynôme nul (qui est de degré par convention, ou considéré comme n'ayant pas de degré) possède une infinité de racines — tout nombre réel est racine de .
Par conséquent :
Les deux polynômes sont identiques, ce qui contredit notre hypothèse initiale qu'ils étaient distincts.
Conclusion
Il ne peut pas exister deux polynômes distincts de degré au plus satisfaisant les conditions de collocation. Le polynôme de collocation est donc unique.
Unicité du polynôme d'interpolation
Démonstration par l'absurde
Étape 1: Hypothèse
Supposons qu'il existe deux polynômes P(x) et Q(x) de degré ≤ n passant par les mêmes n+1 points.
Applications de l'interpolation
L'interpolation polynomiale intervient dans de nombreux domaines :
| Domaine | Application |
|---|---|
| Infographie | Lissage de courbes, animation |
| Traitement du signal | Reconstruction de signaux échantillonnés |
| Calcul numérique | Intégration, dérivation numérique |
| Géodésie | Modélisation du terrain |
| Finance | Courbes de taux d'intérêt |
| Météorologie | Interpolation spatiale des mesures |
Résumé
Dans cette leçon, nous avons établi les fondements de l'interpolation polynomiale :
- L'interpolation estime des valeurs entre les points connus, tandis que l'extrapolation (plus risquée) estime en dehors
- La méthode de collocation construit un polynôme passant exactement par tous les points de données
- Avec points à abscisses distinctes, il existe un unique polynôme de degré au plus satisfaisant les conditions de collocation
- Le théorème d'unicité se démontre par l'absurde : la différence de deux solutions aurait trop de racines
Pour aller plus loin
Dans la prochaine leçon, nous étudierons la formule de Lagrange, une méthode élégante pour construire explicitement le polynôme de collocation sans avoir à résoudre un système d'équations linéaires.